After finishing the page on String Art Math, I decided to reverse the problem and consider families of lines that are tangent to a given curve. Consider a function \(y = f(x)\) that is continuous and differentiable over a range of \(x\). Its derivative is \(y' = f'(x)\) and describes the slope of the curve at every point on the curve. In particular, for some point \((k,f(k))\), a line passing through \((k,f(k))\) with slope \(f'(k)\) will be tangent to the curve described by the function. We can use the slope and point to find the equation of the tangent line. It is \(y = f'(k)x + f(k) - kf'(k)\). We can then use this generic solution to find families of lines tangent to curves described by various common functions.
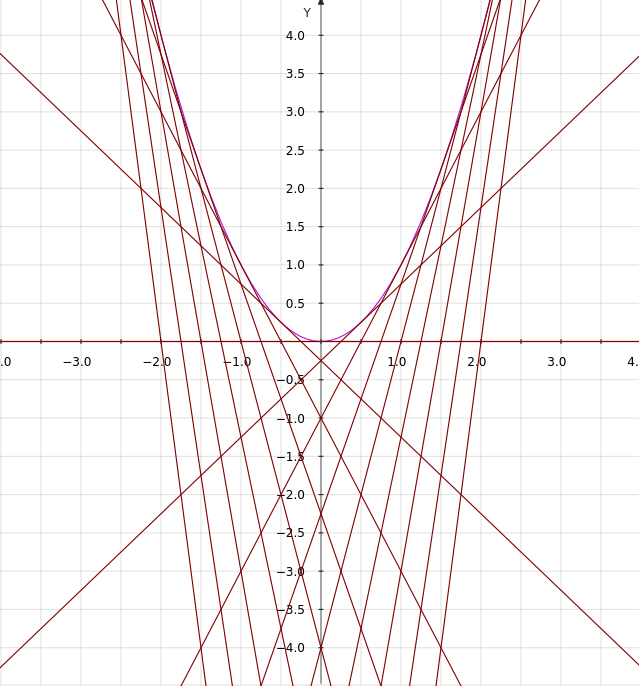
Example 1: \(y = x^2\)
In this case, \(f(x) = x^2\) and \(f'(x) = 2x\). So for some point \((k, k^2)\), the tangent line is \(y = 2kx + k^2 - k(2k)\) or \(y = 2kx - k^2\).
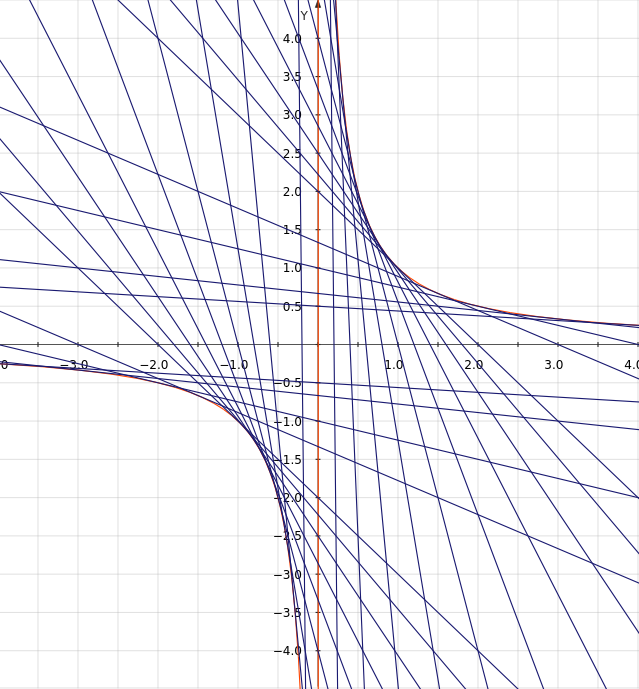
Example 2: \(y = {1 \over x}\)
In this case, \(f(x) = {1 \over x}\) and \(f'(x) = -{1 \over {x^2}}\). So for some point \((k, {1 \over k})\), the tangent line is \(y = -{1 \over k^2}x + {2 \over k}\).
Example 3: \(y = sin(x)\).
In this case, \(f(x) = sin(x)\) and \(f'(x) = cos(x)\). So for some point \((k, sin(k))\), the tangent line is \(y = xcos(k) + sin(k) - kcos(k)\).
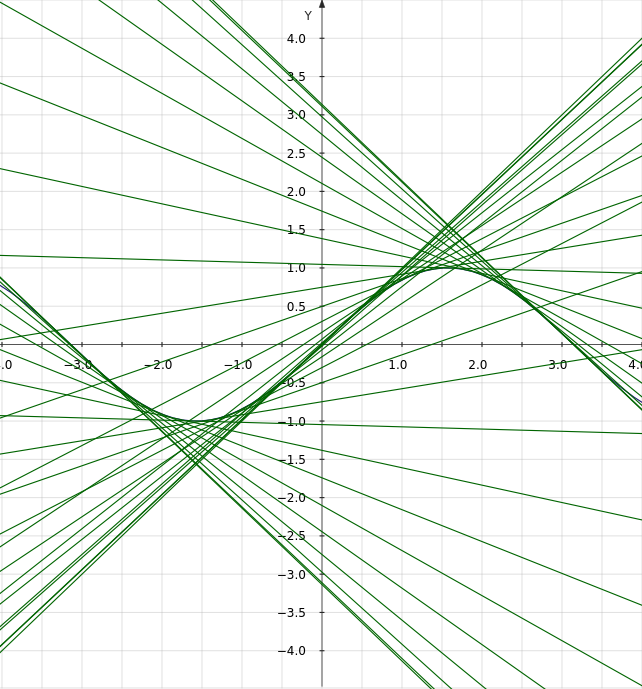
A tool at desmos.com allows you to animate the tangent lines. Here, for example, is an animated graph of the tangent to the sine.