String art produces apparent curves, even though the strings are all
taut. Here is an example. Each string is a line segment, and each line is tangent to a curve.
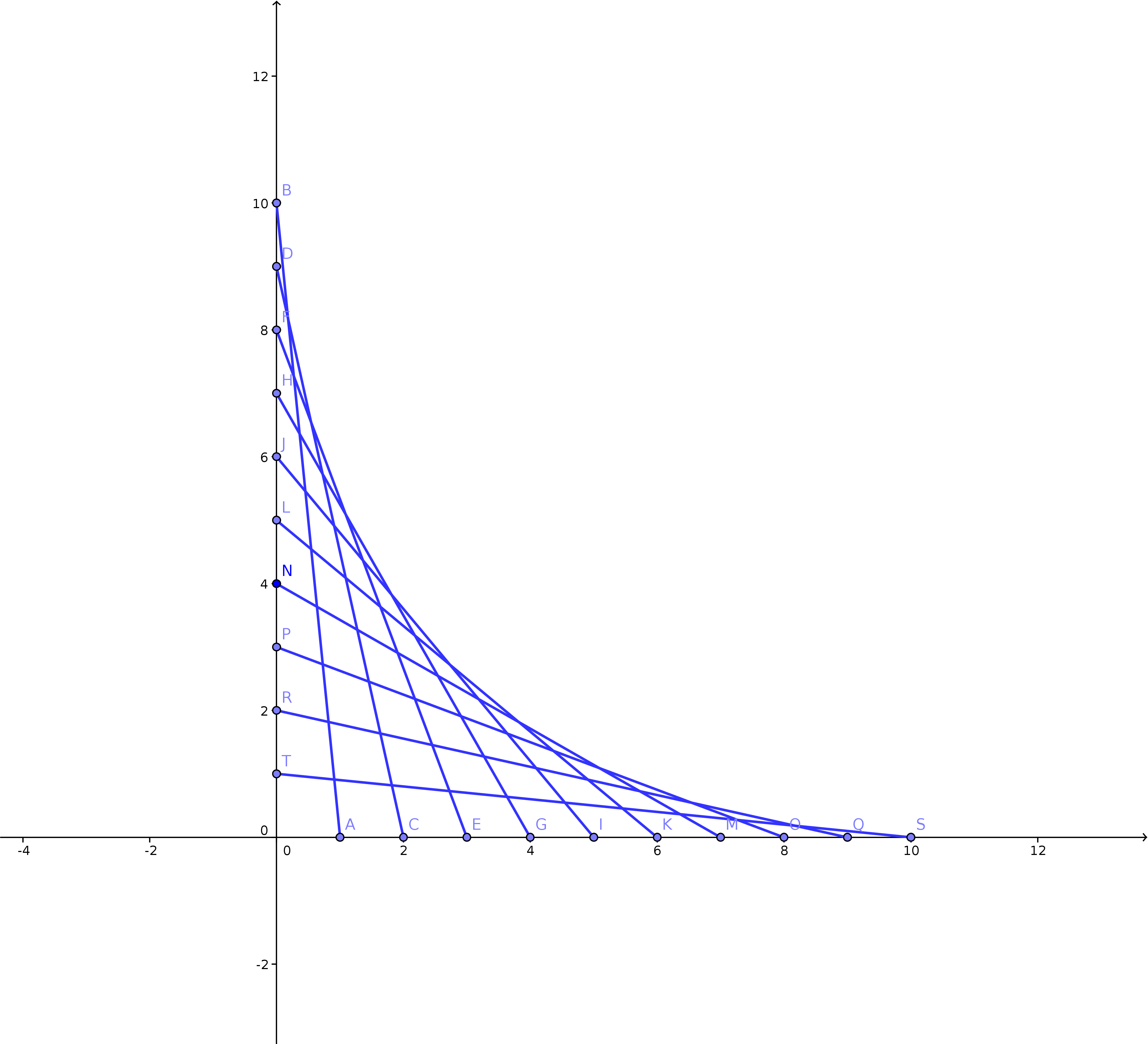Since we have the endpoints of each line, we can determine the equation of each line. For example,
one segment passes through (1, 0) and (0, 10). We can use the two points to determine the
equation of the line. It is \(y = -10x + 10\). For each line, as the point on the \(x\)-axis increases by \(1\),
the corresponding point on the \(y\)-axis decreases by \(1\). Let \((t, 0)\) be a point on the \(x\)-axis. Then
the line passing through that point and point \((0, 11-t)\) on the \(y\)-axis will also be tangent to the same curve. All
the lines shown in the image can be expressed as \(y = {t - 11 \over t}x + (11 - t)\).
To find the curve defined by these lines, let's consider two lines that are very close together. The first line is \(y = {t - 11 \over t}x + (11 - t)\). For the second line, we will substitute \(t + \Delta t\) for \(t\) where \(\Delta t\) is arbitrarily close to \(0\). So the second line will be \(y = {t + \Delta t - 11 \over t + \Delta t} + (11 - t - \Delta t)\). The intersection of these two iines will be very close to the point on the curve where both lines are tangent to the curve. We can find that point by making the expressions equal: $$ {t - 11 \over t}x + (11 - t) = {t + \Delta t - 11 \over t + \Delta t} + (11 - t - \Delta t) $$ Solving for \(x\) gives: $$ x = {{t^2 + t\Delta t} \over 11} $$ Remembering that \(\Delta t\) is close to 0, we can let it get arbitrarily close by finding the limit: $$ \lim_{\Delta t\rightarrow 0} {{t^2 + t\Delta t} \over 11} = {t^2 \over 11}. $$ So \(x = {t^2 \over 11}\). Plugging that value into our original equation, we get \(y = {t^2 \over 11} - 2t + 11\). These two parametric equations define the curve to which the lines are tangent.
We can also eliminate \(t\) and express the curve in terms of \(x\) and \(y\): $$ (x - y)^2 - 22(x + y) + 121 = 0 $$ Solving for \(y\) gives: $$ y = x \pm 2 \sqrt{11x} + 11 $$
The curve is a parabola. Solutions for \(y\) exist only for \(x \ge 0\).