Triangles are the simplest of plane figures1, but they have a number of strange properties. A triangle consists of three line segments such that each endpoint of each segment is shared with one other segment. They can also be viewed as the intersection of three lines, no two of which are parallel.
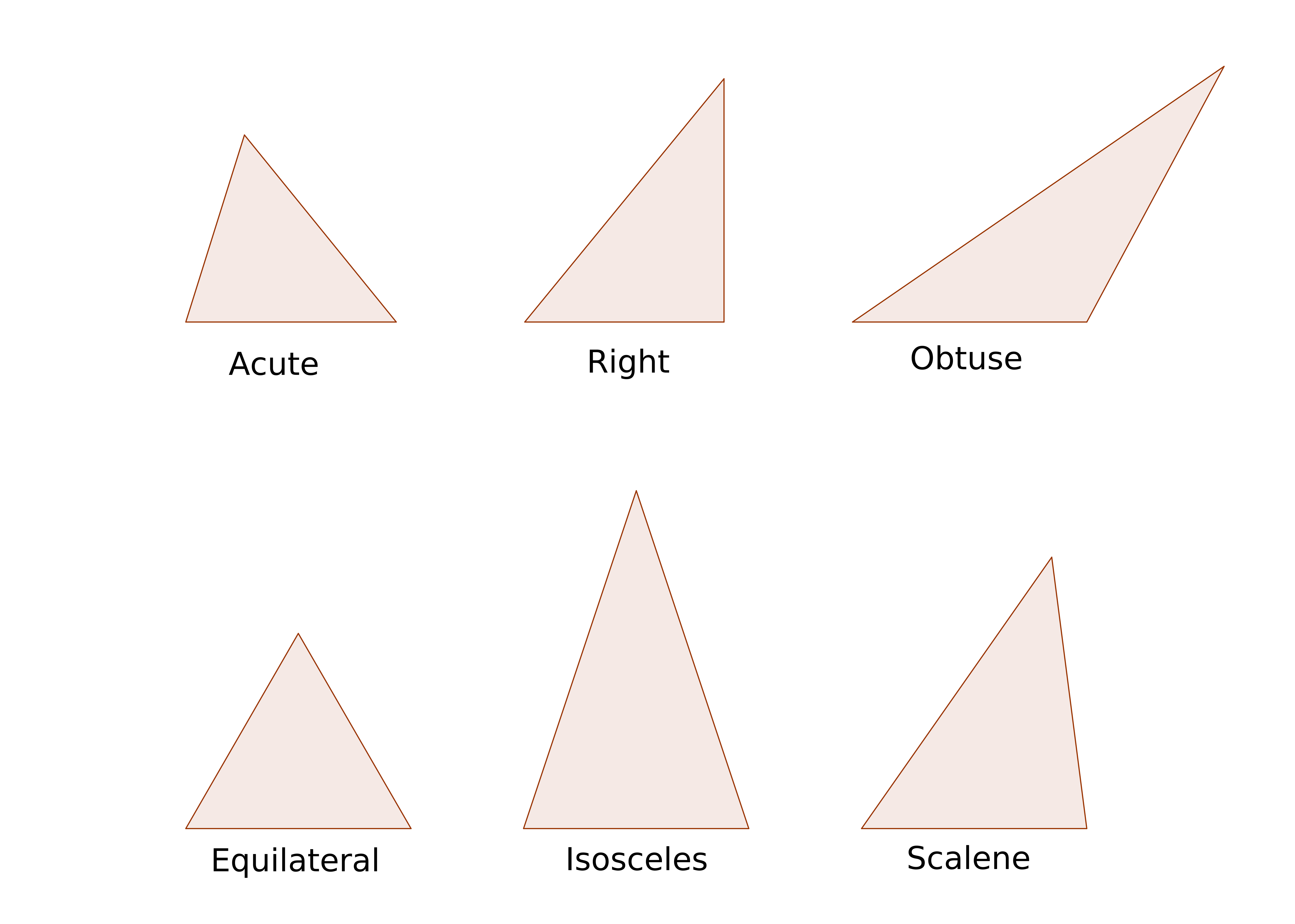
Triangles are classified in two ways: 1) by the measure of their angles, and 2) by how many sides are the same length. Triangles where all the interior angles are less than 90° are called acute triangles. Triangles with one angle of exactly 90° are called right triangles. Triangles with one angle greater than 90° are called obtuse triangles. Different triangles with corresponding angles all measuring the same are called similar triangles. Triangles with all sides the same length are called equilateral triangles. Triangles with just two sides the same length are called isosceles triangles. Triangles with three sides of different lengths are called scalene triangles. Different triangles with corresponding sides all the same length are called congruent triangles. All equilateral triangles have three angles of 60° each, so they are all acute. A right triangle may have two equal sides, making it an isosceles triangle. All isosceles right triangles are similar.
For a triangle to exist, the sum of the lengths of any two sides must exceed the length of the third side. So no triangle exists with sides 1, 2, and 3 units since \(1 + 2 \ngtr 3\). This means that despite their apparent simplicity, triangles can't necessarily be made with three line segments drawn at random. The lengths of any two of the segments must exceed the length of the third no matter how they are considered. Let \(a, b, \)and \(c\) denote the lengths of three sides of a triangle. Then it must be the case that \(a + b \gt c, a + c \gt b,\) and \(b + c \gt a\).
Here's where things get weird. Construct bisectors of each of the three angles. Those three lines meet in a single point.
An angle bisector, as its name implies cuts an angle in half, creating two similar angles, but it is also the locus
of points equidistant from the two lines that make up the angle. So every point on the bisector is the same distance from each side of the
angle. Since the three angle bisectors meet in one point, it follows that that point is the same distance from each side of the triangle.
This point is called the incenter of the triangle, and it can be used to inscribe a circle inside the triangle such that the circle is tangent
to each of the three sides. To construct the circle, drop a perpendicular from the incenter point to each of the sides. Since the incenter
point is equidistant from each side, the lengths of the three perpendiculars are the same and form the radius of the circle.

Just as an angle bisector is equidistant from two lines, a perpendicular bisector of a side of the triangle is equidistant from the endpoints of the side. Construct a perpendicular bisector for each of the three sides. Those three lines also meet in a single point, and that point is equidistant from each of the corners of the triangle. Unlike the intersection of the angle bisectors, the intersection of the side bisectors need not be inside the triangle. In fact, it is inside only if the triangle is acute. For obtuse triangles, the intersection is outside the triangle, and for right triangles, the intersection point lies at the center of the hypotenuse of the right triangle. Lines drawn from this point to the corners are radii of a circle passing through the three corners of the triangle.
You can prove that the perpendicular bisectors meet in a single point because things equal to the same thing are equal to each other. So, for example, consider a triangle \(\triangle ABC\) with sides \(a\) opposite point \(A\), \(b\) opposite point \(B\), and \(c\) opposite point \(C\). Construct perpendicular bisectors through \(a\) and \(b\). Since \(a\) and \(b\) are not parallel, their bisectors also are not parallel and must meet in a point \(P\). The line passing through \(a\) is equidistant from \(B\) and \(C\), so \(P\), which lies on the line, is also equidistant from \(B\) and \(C\). Likewise, the line passing through \(b\) is equidistant from \(A\) and \(C\), and point \(P\) must also be equidistant from \(A\) and \(C\). The only way \(P\) can be equidistant from \(A\) and \(C\) and also from \(B\) and \(C\) is if it is also equidistant from \(A\) and \(B\), which are the endpoints of \(c\). So \(P\) must also lie on the perpendicular bisector of \(c\). Similar reasoning shows that the angle bisectors through \(A\), \(B\), and \(C\) must likewise meet in a single point equidistant from the three sides.
Connecting the midpoints of the sides of any triangle yields four smaller triangles, all congruent and all similar to the larger triangle. So any triangle can be easily cut into four equal area pieces by cutting along the lines connecting the midpoints of the sides. It is also easy to cut any triangle into two equal area pieces. Any line connecting the midpoint of one side to the opposite corner will necessarily cut the triangle into two equal areas. This is because it produces two triangles each with the same height and a base of the same length. Since the area of any triangle is \({1 \over 2}bh\), where \(b\) is the length of the base and \(h\) is the length of the height, the two areas are equal. Another method of dividing a triangle into two equal areas relies on finding the midpoint of the height and constructing a triangle and a quadrilateral from it.
Strangely enough, dividing a triangle into three equal area pieces is a bit more complicated. Begin finding the height and trisecting it. Then construct a parallel through the first point from the base (i. e, \(1/3\) of the height from the base). Do the same for another side. The point where the two parallels intersect is a midpoint in the triangle. Connect it to the three corners, and it forms three triangles. The first has an area of \({1 \over 2}{1 \over 3}b {\sub 1}h {\sub 1} \), which is \(1 \over 3\) the total area of the larger triangle. The second also has an area of \(1 \over 3\) the area of the total area of the larger triangle, even though the base and height are different. This means that the third triangle also has an area \(1 \over 3\) of the total area of the larger triangle.